ML - Frequent Itemset Mining

An association rule is a pattern that states when an event occurs, another event occurs with certain probability. Association relus find all sets of items that have support count greater than the mimimum support; then using the large itemsets to generate the desired rules that have confidence greater than the minimum confidence. For frequent itemset mining, we use Apriori algorithm.

The following details are from The Apriori Algorithm … How The Apriori Algorithm Works.

Concepts

1. A set of all items in a store $I=\{i_1,i_2,…,i_m\}$

2. A set of all transactions (Transaction Database T)

   $T={t_1,t_2,…,t_n}$

3. Each $t_i$ is a set of items s.t. $t\subseteq I$

4. Each transaction $t_i$ has a transaction ID(TID)

基本概念

Apriori Algorithm

Example

Say we have a transaction database and the minimum support count is $sc=2$.

TID	Items
100	1 , 3 , 4
200	2 , 3 , 5
300	1, 2, 3, 5
400	2, 5
500	1, 3, 5

Step One : 1-itemset

Itemset	Support
1	3
2	3
3	4
4	1
5	4

so we delete itemset = 4 because its support is less than 2, after prunning:

Itemset	Support
1	3
2	3
3	4
5	4

Step 2 : 2-itemset

we build 2-itemset based on 1-itemset, where we get {1,2},{1,3},{1,5},{2,3},{2,5},}{3,5}

Itemset	Support
{1,2}	1
{1,3}	3
{1,5}	2
{2,3}	2
{2,5}	3
{3,5}	3

delete itemset { 1,2 } because its support is 1.

Itemset	Support
{1,3}	3
{1,5}	2
{2,3}	2
{2,5}	3
{3,5}	3

Step 3 : 3-itemset

we build 3-itemset based on 2-itemset, where we get{1,3,5},{1,2,3},{1,2,5},{2,3,5}

Before counting each itemset’s support, we do some prunning.

For {1,3,5} : {1,3},{1,5},{3,5}, and according to the fact that any frequent itemsets’ subset must be frequent itemset, so {1,3,5} may be frequent itemset because all of its subsets are frequent itemset.

For {1,2,3} : {1,2},{1,3},{2,3}. Because {1,2} is not frequent itemset, {1,2,3} is not frequent itemset and we don’t need to calculate its support.

Same rule to {1,2,5} and {2,3,5}, we can say that {1,2,5} is not frequent itemset but {2,3,5} may be frequent itemset.

Itemset	Support
{1,3,5}	2
{2,3,5}	2

Step 4 : 4-itemset

we get 4-itemset : {1,2,3,5}.

Prune ：{1,2,3},{1,2,5},{1,3,5},{2,3,5}. because {1,2,5} and {1,2,3} are not frequent itemsets, {1,2,3,5} is not frequent itemset.

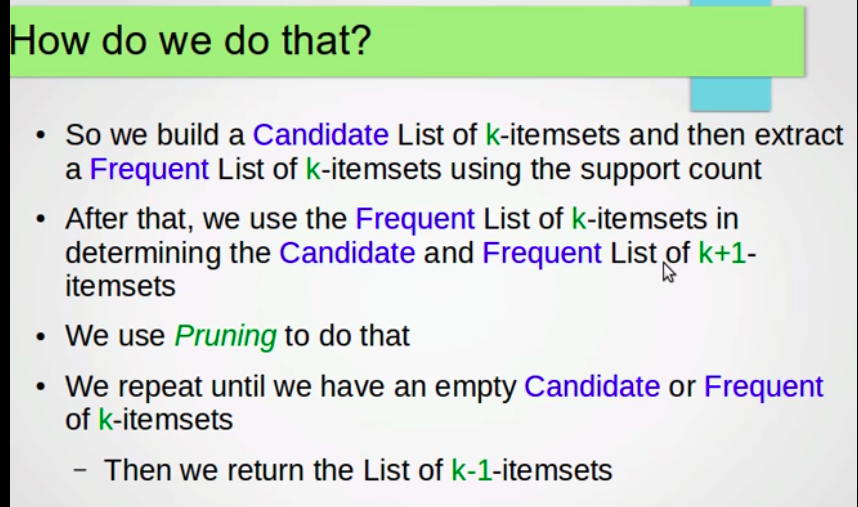
Then we end up with empty. We return 3-itemset {1,3,5} and {2,3,5} for rule generation.

Association rule generation

Now we have the list of frequent itemsets

Itemset	Support
{1,3,5}	2
{2,3,5}	2

Generate all nonempty subsets for each frequent itemset $I$

• For {1,3,5}, we have {1},{3},{5},{1,3},{1,5},{3,5}
• For {2,3,5}, we have {2},{3},{5},{2,3},{2,5},{3,5}

For every subset $s$ of frequent itemset $I$, with the minimum confidence threshold, we generate the rule:

$$s\to(I-s) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if \ \ \ \ \ \frac{sc(I)}{sc(s)}\ge min\_conf$$

Let us assume the minimum confidence threshold is 60%,

For frequent itemset {1,3,5}:

• Rule1: $\{1\}\to \{3,5\}$, confidence = $\frac{sc\{1,3,5\}}{sc\{1\}}=\frac{2}{3}=66.66\%$ Selected
• Rule2: $\{3\}\to \{1,5\}$, confidence = $\frac{sc\{1,3,5\}}{sc\{3\}}=\frac{2}{4}=50\%$ Rejected
• Rule3: $\{5\}\to \{1,3\}$, confidence = $\frac{sc\{1,3,5\}}{sc\{5\}}=\frac{2}{4}=50\%$ Rejected
• Rule4: $\{1,3\}\to \{5\}$, confidence = $\frac{sc\{1,3,5\}}{sc\{1,3\}}=\frac{2}{3}=66.66\%$ Selected
• Rule5: $\{1,5\}\to \{3\}$, confidence = $\frac{sc\{1,3,5\}}{sc\{1,5\}}=\frac{2}{2}=100\%$ Selected
• Rule6: $\{3,5\}\to \{1\}$, confidence = $\frac{sc\{1,3,5\}}{sc\{3,5\}}=\frac{2}{3}=66.66\%$ Selected

Same operations on {2,3,5}.